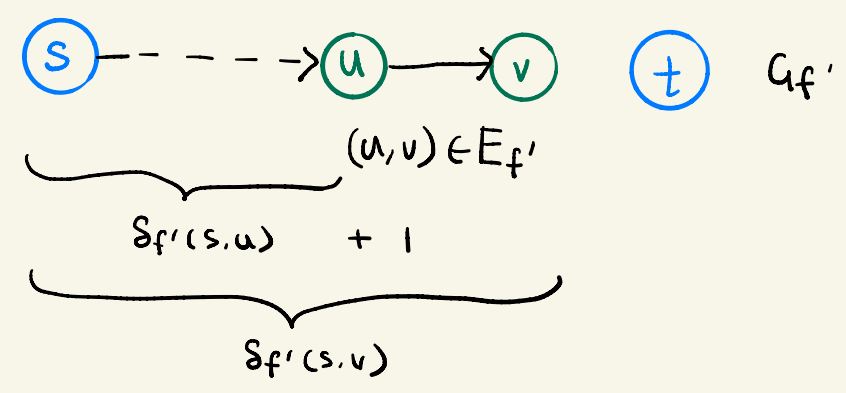NETWORK FLOW

Edmonds-Karp Algorithm finds the augmenting path with BFS.

Which means if we regard each edge as unit distance, we always pick the shortest path from s to t.

It is possible to prove that the runtime of Edmonds-Karp is O(VE²)

Notation: Define δ_f(u,v) for the shortest-path distance from u to v in G_f, where each edge has unit distance

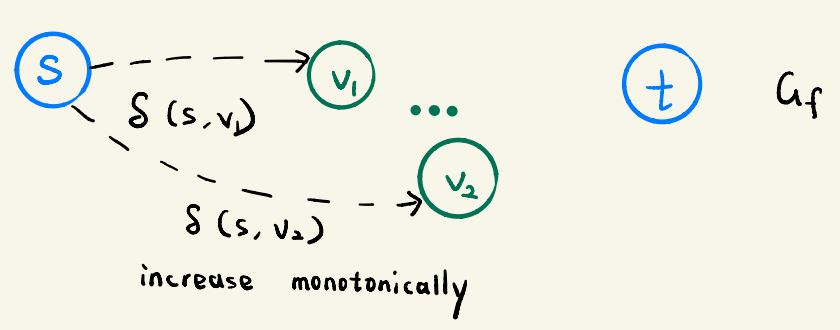
Lemma 26.7: For all vertices v ∈ V - {s,t} the shortest-path distance δ_f(s,v) in residual network increases monotonically with each flow augmentation

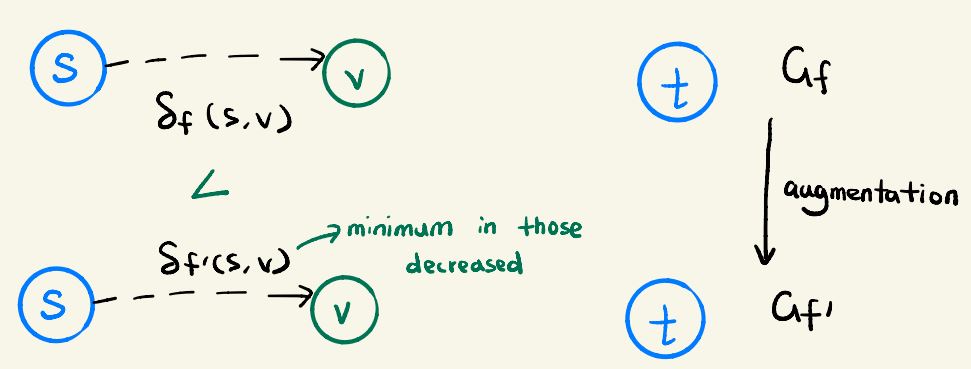
Proof Suppose for sake of contradiction that for some vertex v ∈ V - {s,t} there is a flow augmentation that causes the shortest path distance to decrease.

Let f be the flow just before the augmentation, f' be the one afterwards.

Let v be the vertex with minimum δ_{f '}(s,v) in the set of vertices whose distance was decreased

so that δ_{f '}(u,v) < δ_f(u,v)

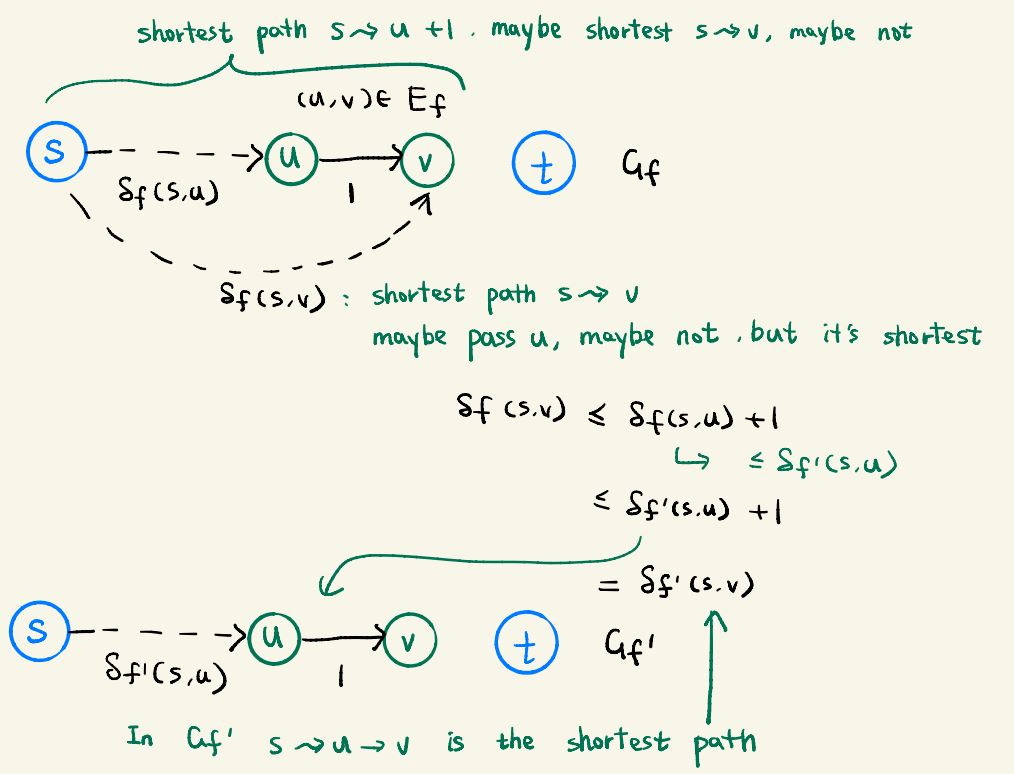
Let p = s ∼ u → v be a shortest path from s to v in G_f',

so that (u,v) ∈ E_f', and δ_{f '}(s,u) = δ_{f '}(s,v) - 1

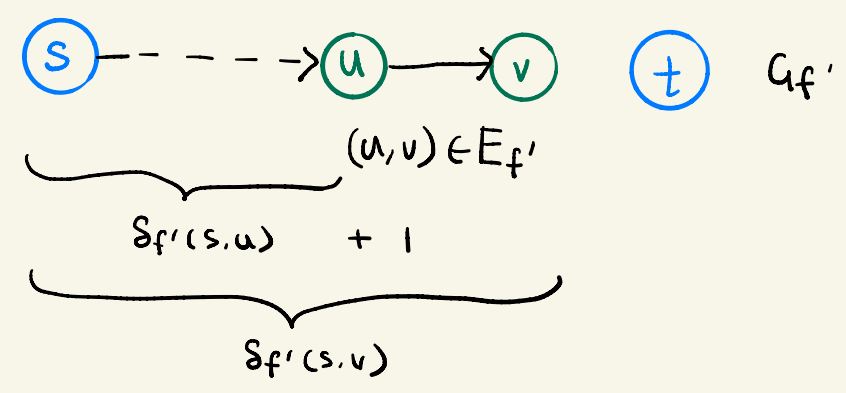
Because we chose v to have the minimum δ_{f '}(s,v) in those decreased,

It is not possible that u has a smaller δ_{f '}(s,u) and it is decreased

And we know s ∼ u → v is a shortest path, thus s ∼ u is also a shortest path which is shorter than s ∼ v.

So if δ(s,u) is decreased, we will have a vertex whose distance was decreased, and also δ_{f '}(s,u) < δ_{f '}(s,v)

Which contradicts with how we chose v as the minimum one.

Since δ_{f '}(s,u) ≤ δ_{f '}(s,v) must be true, the explaination to avoid contradiction is that δ(s,u) doesn't decrease

Which means δ_{f '}(s,u) ≥ δ_f (s,u)

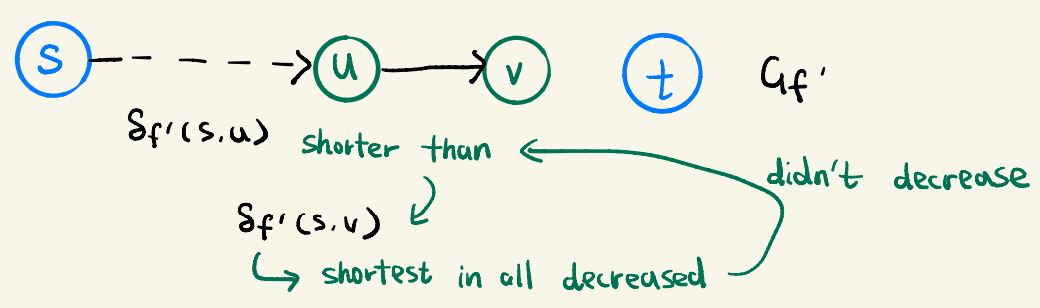
We claim that (u,v) not in E_f. Suppose for sake of contradiction, (u,v) is in E

δ_f(s,v) ≤ δ_f (s,u) + 1

          ≤ δ_{f '}(s,u) + 1

          = δ_{f '}(s,v)

Which contradicts the assumption that δ_{f '}(s,v) < δ_f(s,v)

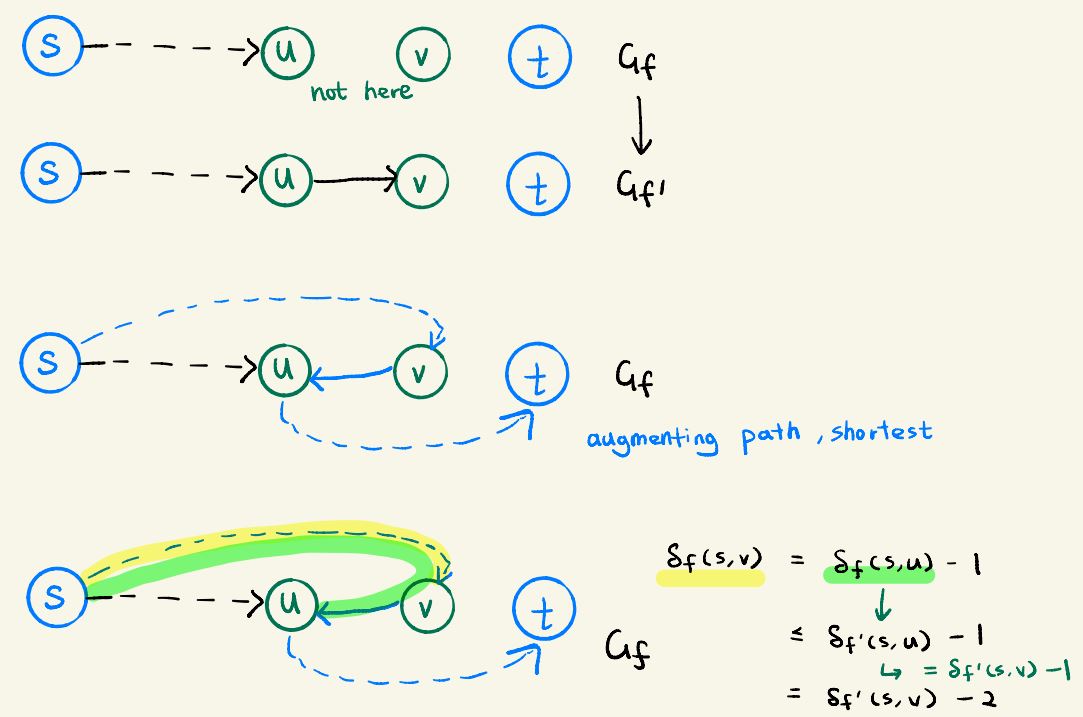
Now we know (u,v) is not in E_f but in E_f'

Which means this edge appears after the augmentation.

This can only happen when the flow from v to u is previously 0 but increased.

Beause Edmonds-Karp always pick the shortest path to augment, so the shortest path from s to u in G_f has (v,u) as last edge

Therefore, δ_f(s,v) = δ_f(s,u) - 1

                            ≤ δ_{f '}(s,u) - 1

                            = δ_{f '}(s,v) - 2

Which contradicts the assumption that δ_{f '}(s,v) < δ_f(s,v)

Thus we conclude our assumption that such a vertex v exists.

And because the smallest one doesn't exist, such vertex that decrease all not exist. Thus the distance cannot decrease.

---

Lemma 26.8: The total number of flow augmentations performed by the algorithm is O(VE)

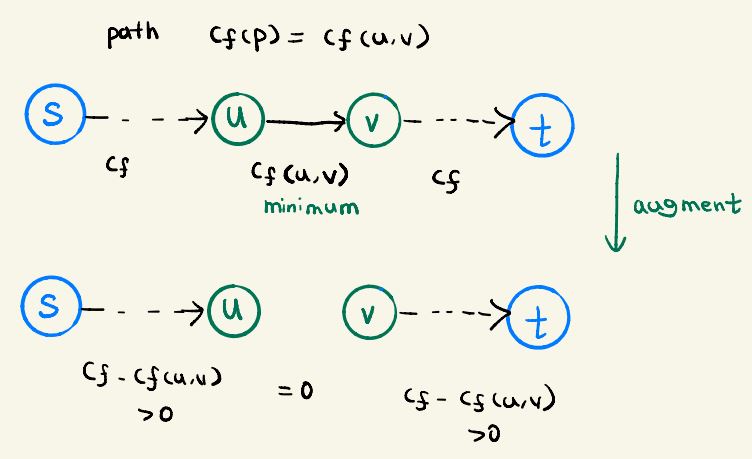
Proof We define an edge (u,v) in residual network as critical on an augmenting path p,

if the residual capacity of p is the residual capacity of (u,v)

That is c_f(p) = c_f(u,v)

After we augmented flow along an augmenting path, any critical edge on the path disappears from the residual network

And also, at least one edge on path p must be critical

We will show that each of the |E| edges can become critical at most |V|/2 times

Let u and v be vertices in V with edge (u,v)

When edge (u,v) is critical for the first time, since we always augment the shortest path, we have:

δ_f(s,v) = δ_f(s,u) + 1

And (u,v) disappears in the residual network.

And it cannot reappear until the flow from u to v is decreased, which occurs when (v,u) appears

Suppose f' is the flow after (u,v) reappear and (v,u) appears, we have:

δ_{f '}(s,u) = δ_{f '}(s,v) + 1

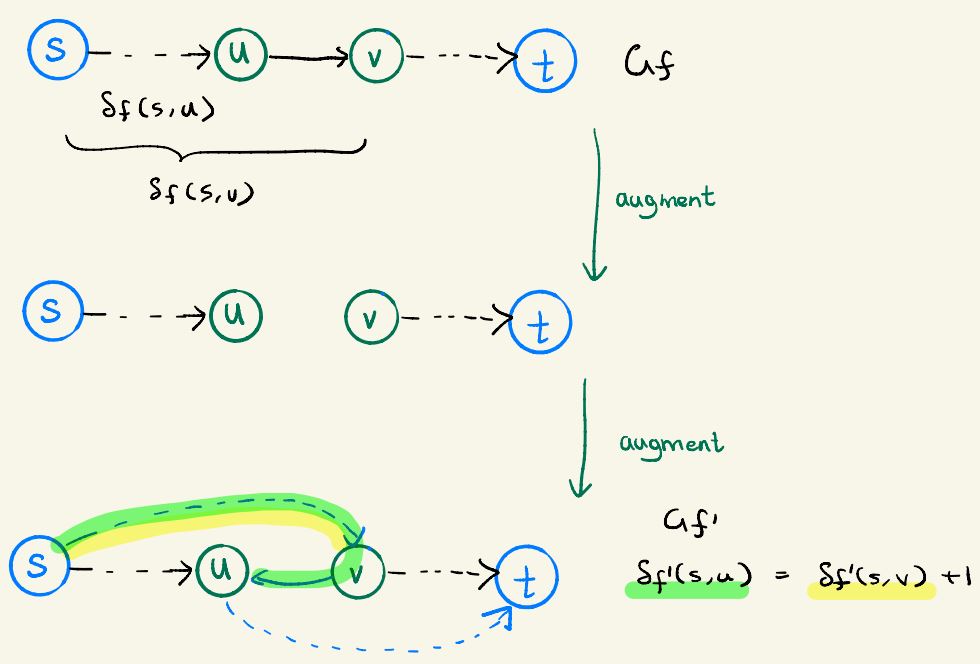
Since δ_f(s,v) ≤ δ_{f '}(s,v) by Lemma 26.7, we have:

δ_{f '}(s,u) = δ_{f '}(s,v) + 1

            ≥ δ_f(s,v) + 1

            = δ_f(s,u) + 2

This means, between the first and next time (u,v) become critical, the distance from s to u increase by at least 2

The distance between s and u is initially 0, and cannot exceed |V|-2 since u is not s or t

Thus it can be critical for at mist |V|-2/2 = |V|/2 -1 times before it is unreachable

Since there're O(E) number of verices, the total number of possible critical edges in all the time is O(VE)