NETWORK FLOW

• Don't send anything back in a loop - that takes capacity play reset
• If there exist any path that we can fill in more capacity - fill more play reset

Residual Network Introduction: Represent how we can change flow in on the edges of G, notation G_f

How much can we change on the flow?

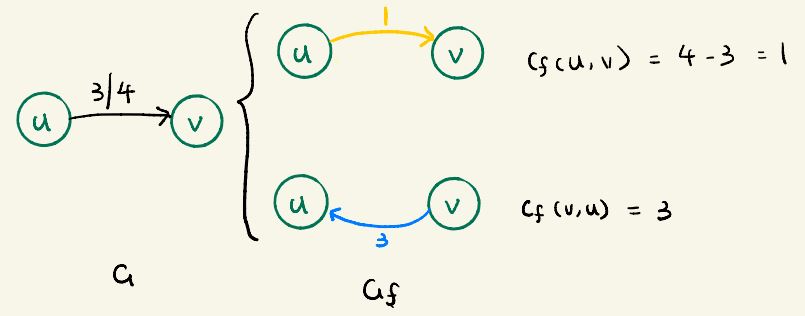
      - Send more on this edge? The possible amount to send more is based on current flow but not exceed current capacity

            c_f(u,v) = c(u,v) - f(u,v)

      - When already sent some flow, what about send less(similar to send the flow back)?

          The amount we can send back is same as current flow, in reversed direction.

            c_f(v,u) = f(u,v)

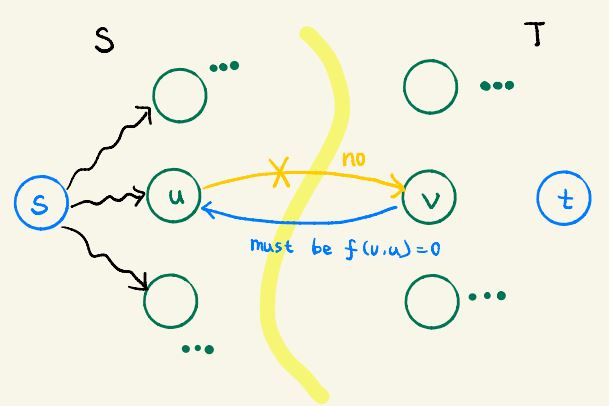
      - Otherwise when there's no edge in G, there's also no change of flow

Residual Network definition:

      Given a flow network G=(V,E) and a flow f. The residual network of G induced by f is G_f=(V, E_f), where

            E_f = { (u,v) ∈ V x V: c_f > 0 }       (Click to see explaination of each part, refresh if a bad color appears)

            The edges in this residual graph are: All possible changes in flow as seen above

Build a residual network here: The part where c_f(u,v) = c(u,v) - f(u,v) The part where c_f(v,u) = f(u,v) Put 2 kinds of lines together Remove edges with weight 0, get residual network reset

Augmentation: A flow in residual network G_f is a hint for adding flow in G

If f is a flow in G and f' is a flow in G_f, we define augmentation:

            (f ↑ f') = f(u,v) + f'(u,v) - f'(v,u)       (Click to see explaination of each part, refresh if a bad color appears)

            The amount we already sent in flow f from u to v The amount we send more in f' from u to v The amount we send back in f' from v to u

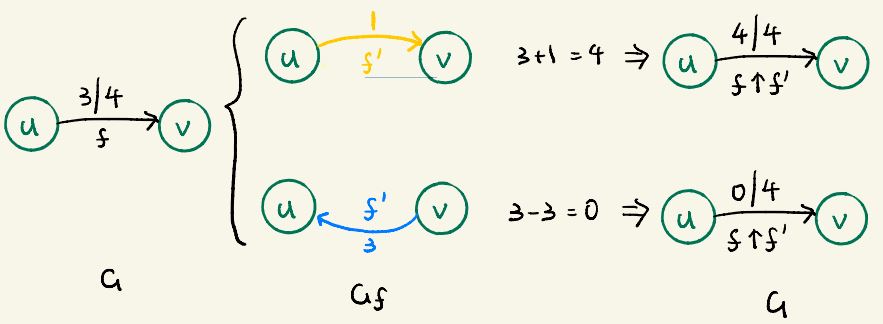
Lemma 26.1 |f ↑ f'| = |f| + |f'| WHY?

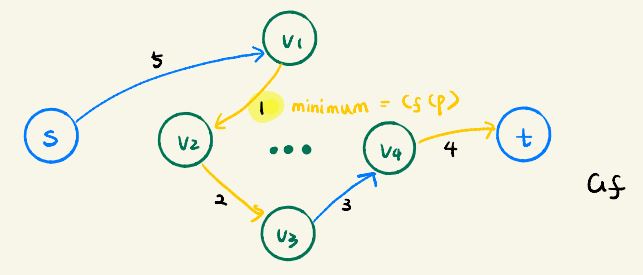
Augmenting Path: A simple path from s to t in the residual network G_f

Residual Capacity: The maximum amount by which we can increase the flow on each edge in an augmenting path p.

            c_f(p) = min { c_f(u, v): (u, v) is on p }       (Click to see explaination of each part, refresh if a bad color appears)

            The maximum amount we can increase without violating anything on this path is to incerase it by smallest residual value of all edges All the edges on path

Cut: A cut(S, T) of flow network G is a partition of V into 2 parts:

      S, which contains supply s;

      T, which contains target t

Net Flow: If f is a flow, the net flow(S, T) across the cut(S, T) is defined to be:

      f(S,T) = ∑ _{u ∈ S} ∑ _{v ∈ T} f(u,v)   -   ∑ _{u ∈ S} ∑ _{v ∈ T} f(v,u)     (Click to see explaination of each part, refresh if a bad color appears)

All nodes in part S All nodes in part T Sum up the flow from nodes in S to nodes in T All nodes in part S All nodes in part T Sum up the flow from nodes in T to nodes in S

Net Flow on Example cuts: cut 1 cut 2 cut 3 cut 4 reset

Observation(Lemma 26.4): The net flow acorss any cut is the same, which equals the value of the flow WHY?

Capacity of cut: The capacity of cut(S, T) is sum of capacity of edges from node in set S to T

      c(S,T) = ∑ _{u ∈ S} ∑ _{v ∈ T} c(u,v)     (Click to see explaination of each part, refresh if a bad color appears)

All nodes in part S All nodes in part T Sum up the capacity from nodes in S to nodes in T

Capacity on example cuts: cut 1 cut 2 cut 3 cut 4 reset

Minimum Cut: A cut whose capacity is minimum over all cuts of the network

Corollary 26.5: The value of any flow f in a flow network G is bounded from above by the capacity of any cut of G. WHY?

Content: If f is a flow in a flow network G=(V,E) with source s and sink t, then the following conditions are equivalent:

      1. f is a maximum flow in G

      2. The residual network G_f contains no augmenting paths.

      3. |f| = c(S,T) for some cut(S,T) of G.

Proof: 1 ⇒ 2

      Suppose for the sake of contradiction that f is maximum flow in G, but G_f has an augmenting path p.

      Then, by Corollary 26.3WHY?, if we augment f by f_p we can get a flow |f ↑ f_p| strictly greater than |f|

      That contradicts the the assumption that f is a maximum flow

Proof: 2 (No augmenting path) ⇒ 3 (Flow = capacity of some cut)

      Suppose G_f has no augmenting path, that is same as G_f contains no path from s to t.

      Define S={ v ∈ V: there exist a path from s to v in G_f }

      And T - V - S, that is the vertices for which there's no path from s to them

      This partition must be a cut, since we already know there's no path from s to t thus t is in set T.

      Consider a pair of vertices u ∈ S and v ∈ T.

      If there's an edge from u to v, we must have f(u,v) = c(u,v)

        Because if we have f(u, v) ≤ c(u, v), this flow can possibly be raised

        If it is possible to raise it, then there's an edge c_f from u to v = c(u,v) - f(u,v)

        In this way v is reachable from u, which means v is reachable from s, and v should be in set S,
        which contradicts the assumption that v is in T

      If there's an edge from v to u, we must have f(v,u) = 0

        Because if we have f(u, v) ≠ 0, it is possible to send flow back from u to v in c_f

        Same idea, in this way v is reachable from s.

      Thus we have:

      f(S,T) = ∑ _{u ∈ S} ∑ _{v ∈ T} f(u,v)   -   ∑ _{u ∈ S} ∑ _{v ∈ T} f(v,u)

                          Network flow definition

              = ∑ _{u ∈ S} ∑ _{v ∈ T} c(u,v)   -   ∑ _{u ∈ S} ∑ _{v ∈ T} 0

                          We just proved f(u,v) = c(u,v) We proved f(v,u) = 0

              = c(S, T)

                          By definition of cut

      Then, by Lemma 26.4WHY?, |f| = f(S,T) = c(S,T)

Proof: 3 (Flow = capacity of some cut) ⇒ 1 (Is a max flow)

      By by Corollary 26.5WHY? |f| ≤ c(S, T) for all cuts (S, T). The condition |f| = c(S, T) implies that f is a maximum flow.